Є одна дуже цікава задача мого дитинства - задача про "цілочисельний паралепіпед".
Прямокутний паралепіпед, в якого є 7 невідомих:
3 ребра, 3 його лицьові діагоналі, 1 просторова діагональ.
Задача полягає, чи існує такий паралепіпед, в якого всі 7 вказаних змінних є цілими числами?
Задача еквівалента вирішенню системи діафантових рівнянь:
a2+b2=d2
a2+c2=e2
b2+c2=f2
b2+e2=g2
Станом на 1988 задача не була вирішена, як і не було доведено, що рішення не існує.
Пропоную організувати прямий розумний перебір.
Беремо 3 натуральних числа a, b и c, такі, що
a < b < c,
a+1 <= b <= (a^2-4)/4,
b+1 < с <= (a^2-1)/2
Для кожного а організовуємо 2 вкладені цикли:
for b = (a + 1) to int((a^2 - 4)/4)
if checkab(a, b) <> 0 then
d = checkz(a, b)
if d <> 0 then
for c = (b + 1) to int((a^2 - 1)/2)
if checkabc(a, b, c) <> 0 then
e = checkz(a, c)
if e <> 0 then
f = checkz(b, c)
if f <>0 then
g = checkz(b, e)
if g <> 0 then addresult(a, b, c, d, e, f, g)
endif
endif
endif
endif
endfor
endif
endif
endfor
В функції checkab(a, b) перевіряємо, що a і b не є одночасно непарними.
В функції checkabc(a, b, c) перевіряємо, що:
1. серед a, b і c тільки одне число непарне.
2. одне з чисел ділить на 4, а одне з інших - на 16
3. одне з чисел ділить на 3, а одне з інших - на 9
4. одне з чисел ділить на 5
5. одне з чисел ділить на 7
6. одне з чисел ділить на 9
7. одне з чисел ділить на 11
8. одне з чисел ділить на 19
В функції checkz(x, y) перевіряємо, чи існує натуральне z, таке, що
x2+y2=z2. Якщо не існує, повертаємо 0. Існує - звісно повертаємо z.
Тут є декілька думок:
Перша - перевірка останньої цифри суми квадратів.
Оскільки остання цифра квадрату може бути:
1 - 1
2 - 4
3 - 9
4 - 6
5 - 5
6 - 6
7 - 9
8 - 4
9 - 1
0 - 0
Отже квадрат може закінчуватись тільки на (0, 1, 4, 5, 6, 9), а сума квадратів може приймати значення з імовірностями:
0 - 16,67%
1 - 11,11%
2 - 5,56%
3 - 5,56%
4 - 11,11%
5 - 16,67%
6 - 11,11%
7 - 5,56%
8 - 5,56%
9 - 11,11%
Отже, ще до будь-яких піднесень до квадратів можна одразу відкинути 2/9 всіх пар чисел.
Ще один випадок, що можна швиденько відкинути: якщо остання цифра суми квадратів закінчується на 0, шуканий квадрат має закінчуватись на 00.
Задля цієї перевірки достатньо перевірити:
k = x rem 100
l = y rem 100
тобто k і l - числа, складені з двох останніх цифр x та y відповідно.
Тоді треба перевірити, що
(k^2 + 2k + l^2 + 2l) rem 100 = 0
Ну а далі треба шукати швидкі методи пошуку натуральних коренів.
Поки що все.
P.S.: Процедура addresult() зберігає результат і виплачує премію в 1000 дол.

P.P.S.: Почитав пости назад у часі... ідея з пошуком "ідеального кубоіда" вже була, тільки що brute force без особливих оптимізацій.
Тому вибачаюсь за повтор. Витирати посилання не буду, оскільки приклав багато зусиль, щоб все викласти, що в голові було.
P.P.P.S: якщо є обчислювальні обмеження з точним обрахунком квадрату числа (можу припустити, що так воно і є), можу запропонувати організацію вкладених циклів в оберненому порядку від більшого числа до меншого.
Тобто спочатку фіксуємо найбільше з ребер c, потім організовуємо цикл вниз від (с-1) до int(sqrt(4c+4)) для числа b, ну а потім цикл вниз від (b-1) до int(sqrt(2c+1)) для найменшого з ребер a.
Ну а все інше - як викладено вище.
На вхід подається 2 числа, m і n:
m <= c <= n
for c = m to n
for b = (с - 1) downto int(sqrt(4c + 4))
if checkab(b, c) <> 0 then
f = checkz(b, c)
if f <> 0 then
for a = (b - 1) downto int(sqrt(2c+1))
if checkabc(a, b, c) <> 0 then
d = checkz(a, b)
if d <> 0 then
e = checkz(a, c)
if e <>0 then
g = checkz(b, e)
if g <> 0 then addresult(a, b, c, d, e, f, g)
endif
endif
endif
endif
endfor
endif
endif
endfor
endfor
Числа m і n визначають, як вся задача розрізається на окремі завдання.
Вартість завдання можна визначати, наприклад:
1. за кількістю заходів в checkz
2. за кількістю нетривіальних перевірок в середині checkz (алгоритм якої ще треба придумати).
3. за кількістю заходів в checkab
4. за кількістю заходів в checkabc
Всі 4 числа мають різну вагу, тому що складність виконання різна.
Валідність розрахунку можна визначати теж за цим показником.
(Rilian @ Aug 6 2010, 01:47)

я эту задачу уже рассматривал, не зря тестовый боинк висел у нас на поддомене cuboid

)
потом почитал новости по теме, там уже перебрали немеряное кол-во чисел, и для больших ничего не нашли
А в мене з дитинства залишилась віра, що, якшо знайшли майже ідеальний паралелепіпед (6 з 7 - натуральні),
то має бути і повністю ідеальний цеглоїд.

Всі 7 величин! 7 - це Боже число. Як знайдемо, то кінець світу настане!

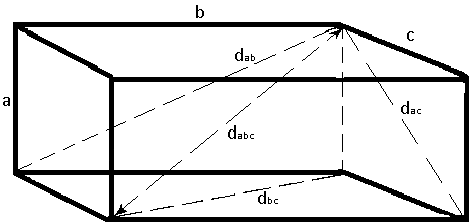

 — одна з лицевих діагоналей не ціле число.
— одна з лицевих діагоналей не ціле число. ,
,  — одне з ребер не ціле число.
— одне з ребер не ціле число.