 Generalized Woodall Numbers |
Привіт Гість ( Вхід | Реєстрація )
|
  |
| nikelong |
 Feb 9 2009, 20:52
Пост
#1
|
 Тера ранчер  Група: Trusted Members Повідомлень: 11 909 З нами з: 19-March 05 Користувач №: 92 Стать: Чол  |
 Generalized Woodall Numbers http://www.geocities.com/harvey563/General...odallPrimes.txt http://www.rechenkraft.net/wiki/index.php?...Woodall_Numbers Це повідомлення відредагував nikelong: Mar 9 2009, 22:04 |
   |
 
|
| Death |
Feb 10 2009, 11:49
Пост
#2
|
 <script ///> Група: Moderators Повідомлень: 6 371 З нами з: 5-November 03 З: Kyiv Користувач №: 26 Стать: НеСкажу Free-DC_CPID Парк машин: гидропарк jabber:deadjdona@gmail.com |
Primes of the form n*b^n-1, n>b-2, b>2
-------------------- |
|
|
|
wbr, Me. 
Dead J
| nikelong |
Feb 22 2009, 20:51
Пост
#3
|
|
Тера ранчер Група: Trusted Members Повідомлень: 11 909 З нами з: 19-March 05 Користувач №: 92 Стать: Чол |
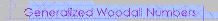 Количество участников - 11 (!!) http://science.kennesaw.edu/~jdemaio/generali.htm The Generalized Woodall Numbers project found generalized Woodall numbers using the Proth program. --------------------   |
|
|
|
|
|
|
1 Користувачів переглядають дану тему (1 Гостей і 0 Прихованих Користувачів)
0 Користувачів:
|
Lo-Fi Версія | Поточний час: 4th November 2025 - 02:43 |