Perfect Cuboid, Задача про цілочисельний паралелепіпед Налаштування

[x3mEn]

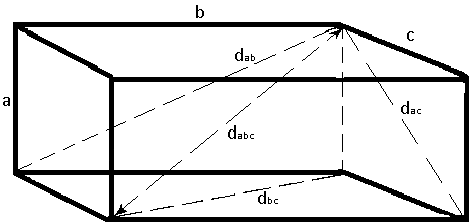Раціональний кубоїд (або цілочисельна цеглина, або ідеальний кубоїд) — прямокутний паралелепіпед,
у якого всі сім основних величин (три ребра, три лицьових діагоналі і просторова діагональ) є цілими числами, є однією з відкритих математичних проблем
Інакше кажучи, раціональний кубоїд — цілочисельне рішення системи діофантових рівнянь.

Досі невідомо, чи існує такий паралелепіпед. Комп'ютерний перебір не знайшов жодної цілочисельної цеглини з ребрами до 10^11.
Втім, знайдено кілька «майже цілочисельних» паралелепіпедів, у яких цілочисельними є всі величини, крім однієї:
— одна з лицевих діагоналей не ціле число.
, — одне з ребер не ціле число.
Велика кількість паралелепіпедів Ейлера (з нецілою просторовою діагоналлю, див. нижче).
Косокутні паралелепіпеди, у яких всі сім величин цілі. При цьому досить одного непрямого кута.
У 2005 році тбіліський студент Лаша Маргішвілі запропонував доведення, що цілочисельний кубоід не існує — однак на 2009 рік робота так і не пройшла перевірку незалежними вченими.

Паралелепіпед Ейлера
Прямокутний паралелепіпед, у якого цілочисельні тільки ребра і лицьові діагоналі, називається ейлеровим.
Найменший з паралелепіпедів Ейлера — (240, 117, 44), з лицьовими діагоналями 267, 244 і 125.
Ще кілька паралелепіпедів Ейлера:
(275, 252, 240),
(693, 480, 140),
(720, 132, 85),
(792, 231, 160).
Ейлер описав два сімейства таких паралелепіпедів (звідси назва). Втім, повного опису всіх паралелепіпедів Ейлера також немає.
Відомі такі вимоги до ейлерового паралелепіпеда (а значить, і до цілочисельної цеглини):
- Одне ребро ділиться на 4, друге ділиться на 16, третє непарне (якщо, звичайно, він примітивний — тобто, НСД (a, b, c) = 1).
- Одне ребро ділиться на 3 і ще одне — на 9.
- Одне ребро ділиться на 5.
- Одне ребро ділиться на 11.
- Одне ребро ділиться на 19.
- Одне ребро або просторова діагональ діляться на 13.
- Одне ребро, лицьова або просторова діагональ діляться на 17.
- Одне ребро, лицьова або просторова діагональ діляться на 29.
- Одне ребро, лицьова або просторова діагональ діляться на 37.
- Добуток ребер, лицьових і просторової діагоналі має ділитися на 2^8·3^4·5^3·7·11·13·17·19·29·37

Це повідомлення відредагував x3mEn: Oct 22 2013, 09:16

[rpisarev]

Death,
до задачі по Perfect Cuboid мені вдалося долучити Andrii Muliar.
Він дуже сильно вплинув на моє бачення реалізації проекту.
Зокрема він мене переконав, що прямий перебір діагоналей - не така вже витратна операція
Я планував влаштувати генерацію діагоналей як добуток простих чисел 4k+1 у всіх можливих комбінаціях (добуток менший за наперед задане число (2^63-1)).
Але, по-перше, такий перебір наврядчи буде завершено для всіх чисел з діапазону (2; 2^63-1), навіть за умови, що вони є добутком простих чисел 4k+1 (надто вже багато просто протих чисел виду 4k+1, а для утворення діагоналі-кандидата достатньо домножити це просте на 5 (5 - мінімальне просте виду 4k+1). А простих чисел 4k+1, таких, що 5*(4k+1) < 2^63-1 ну дуже вже багато).
А по-друге, результат проекту за такого пошуку буде звучати приблизно так:
Якщо ідеальний кубоїд існує і його просторова діагональ менша за 2^63, ця діагональ у своєму розкладі на дільники має містити фактор, що більший за 2^36.
Це звучить не дуже зрозуміло, чи не так, порівняно, наприклад, з таким результатом:
Якщо ідеальний кубоїд існує, його просторова діагональ більша за 2^36.
Такий результат проекту більш зрозумілий, чи не так?

Якщо в деталях,
на цей момент і з його, і з мого боку написані програми, які вміють:
1) перебирати діапазони чисел, розкладати числа на дільники, відсіюючи таким чином, що залишаються тільки ті числа, які є добутком простих чисел виду 4k+1.
2) розкладають ці прості числа на суми квадратів. На цей момент це досить витратна операція. Ми плануємо її оптимізувати
3) будує всі можливі розклади квадрата вихідного числа на всі можливі суми квадратів
4) шукає серед отриманих розкладів:
-- примітивні майже ідеальні кубоїди, в яких із 7-ми розмірностей не ціла тільки одна сторона
-- примітивні майже ідеальні кубоїди, в яких із 7-ми розмірностей не ціла тільки лицьова діагональ
-- ну і власне примітивні ідеальні кубоїди (якщо такі будуть)

А я вот в отпуске снова вчера копнул в тот джава код, почитал описание автора с точки зрения математики и сходу смог написать представления 4k+1 в виде 2 квадратов и 4k+3 в виде 4-х. Скорость декомпозиции 4k+1 сводится к алгоритму разрешимости квадратичного сравнения x^2 = -1 (mod 4k+1), т.е. по сути нахождению корня из -1 в поле Z(4p+1). Пока сделал "в лоб" - перебором: математика не знает лучших методов. Но функция нахождения корня параметр, т.е. в последствии можно бесшовно заменить. Известно лишь, что их 2, один четный, второй нечетный. Надо поискать результаты современной математики - может есть быстрый алгоритм.

Так же есть функция, которая принимает 2 числа, умеет их разложить в декомпозицию 4-х (в общем случае) квадратов и выдать ответ - декомпозиция в виде 4-х квадратов от произведения двух чисел. Понятно её можно обобщить на большее число.

Алгоритма факторизации пока нет и не уверен, что успею до конца отпуска.

Сейчас это консольная программа на Python, за день-два могу переписать на Си/Си++ (без длинной арифметики). Пока начал разбираться с общем случаем представления (хотя для решения задачи перфекткуба, кажется, это и не надо)