Perfect Cuboid, Задача про цілочисельний паралелепіпед Налаштування

[x3mEn]

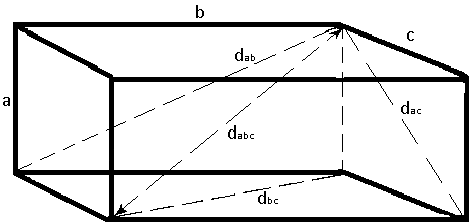Раціональний кубоїд (або цілочисельна цеглина, або ідеальний кубоїд) — прямокутний паралелепіпед,
у якого всі сім основних величин (три ребра, три лицьових діагоналі і просторова діагональ) є цілими числами, є однією з відкритих математичних проблем
Інакше кажучи, раціональний кубоїд — цілочисельне рішення системи діофантових рівнянь.

Досі невідомо, чи існує такий паралелепіпед. Комп'ютерний перебір не знайшов жодної цілочисельної цеглини з ребрами до 10^11.
Втім, знайдено кілька «майже цілочисельних» паралелепіпедів, у яких цілочисельними є всі величини, крім однієї:
— одна з лицевих діагоналей не ціле число.
, — одне з ребер не ціле число.
Велика кількість паралелепіпедів Ейлера (з нецілою просторовою діагоналлю, див. нижче).
Косокутні паралелепіпеди, у яких всі сім величин цілі. При цьому досить одного непрямого кута.
У 2005 році тбіліський студент Лаша Маргішвілі запропонував доведення, що цілочисельний кубоід не існує — однак на 2009 рік робота так і не пройшла перевірку незалежними вченими.

Паралелепіпед Ейлера
Прямокутний паралелепіпед, у якого цілочисельні тільки ребра і лицьові діагоналі, називається ейлеровим.
Найменший з паралелепіпедів Ейлера — (240, 117, 44), з лицьовими діагоналями 267, 244 і 125.
Ще кілька паралелепіпедів Ейлера:
(275, 252, 240),
(693, 480, 140),
(720, 132, 85),
(792, 231, 160).
Ейлер описав два сімейства таких паралелепіпедів (звідси назва). Втім, повного опису всіх паралелепіпедів Ейлера також немає.
Відомі такі вимоги до ейлерового паралелепіпеда (а значить, і до цілочисельної цеглини):
- Одне ребро ділиться на 4, друге ділиться на 16, третє непарне (якщо, звичайно, він примітивний — тобто, НСД (a, b, c) = 1).
- Одне ребро ділиться на 3 і ще одне — на 9.
- Одне ребро ділиться на 5.
- Одне ребро ділиться на 11.
- Одне ребро ділиться на 19.
- Одне ребро або просторова діагональ діляться на 13.
- Одне ребро, лицьова або просторова діагональ діляться на 17.
- Одне ребро, лицьова або просторова діагональ діляться на 29.
- Одне ребро, лицьова або просторова діагональ діляться на 37.
- Добуток ребер, лицьових і просторової діагоналі має ділитися на 2^8·3^4·5^3·7·11·13·17·19·29·37

Це повідомлення відредагував x3mEn: Oct 22 2013, 09:16

[x3mEn]

Дедлайн збільшено до 5 днів.
За 7 днів підпроект, стартувавши з 10Т, вже перевищив 70Т.
При цьому утворюючи неперевний діапазон (як мінімум) двічі перевірених чисел від 10Т до 31Т.
Нагадаю, що мануальний кранч досяг 30Т десь приблизно за 2 місяці.
Як то кажуть — відчуйте різницю.

Підпроект набирає оберти. Це видно за графіком Unsent tasks.
Графік стабілізувався, була помилка із оцінкої складності завдання (заменшена у 30 разів), через що на самому початку проекту клієнти від сервера отримували більше завдань, ніж ті здатні порахувати до дедлайну.
Тепер все ґаразд, кількість активних юзверів день від дня зростає.

Результати мануального кранчу, якій закінчився/призупинився позавчора:
40'730 tasks done
38'115 hours = 1588 days = 4,348 years spent
30'359'586'957'394 achieved
—-------------------------------------------------
0 perfect cuboids found
74'706 edge cuboids found
129'983 face cuboids found
0 perfect complex cuboids found
313'393 imaginary cuboids found
1'554'246 twilight cuboids found

Я вдячний всім, хто приймав участь у альфа тестуванні і допоміг зробити програму кращою, а це:
A1ex01
rpisarev
5erg
dimus8210
vasyannyasha
firstomega
(_KoDAk_)

Даю посилання на групу в Telegram, якщо будуть якісь питання чи потрібна допомога:
https://t.me/joinchat/BrFEbg7IlqMFl4PBRSdEBA