Perfect Cuboid, Задача про цілочисельний паралелепіпед Налаштування

[x3mEn]

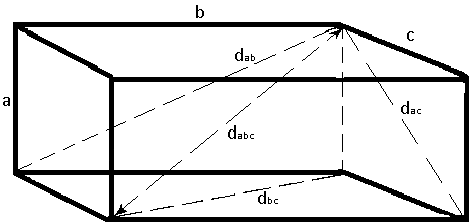Раціональний кубоїд (або цілочисельна цеглина, або ідеальний кубоїд) — прямокутний паралелепіпед,
у якого всі сім основних величин (три ребра, три лицьових діагоналі і просторова діагональ) є цілими числами, є однією з відкритих математичних проблем
Інакше кажучи, раціональний кубоїд — цілочисельне рішення системи діофантових рівнянь.

Досі невідомо, чи існує такий паралелепіпед. Комп'ютерний перебір не знайшов жодної цілочисельної цеглини з ребрами до 10^11.
Втім, знайдено кілька «майже цілочисельних» паралелепіпедів, у яких цілочисельними є всі величини, крім однієї:
— одна з лицевих діагоналей не ціле число.
, — одне з ребер не ціле число.
Велика кількість паралелепіпедів Ейлера (з нецілою просторовою діагоналлю, див. нижче).
Косокутні паралелепіпеди, у яких всі сім величин цілі. При цьому досить одного непрямого кута.
У 2005 році тбіліський студент Лаша Маргішвілі запропонував доведення, що цілочисельний кубоід не існує — однак на 2009 рік робота так і не пройшла перевірку незалежними вченими.

Паралелепіпед Ейлера
Прямокутний паралелепіпед, у якого цілочисельні тільки ребра і лицьові діагоналі, називається ейлеровим.
Найменший з паралелепіпедів Ейлера — (240, 117, 44), з лицьовими діагоналями 267, 244 і 125.
Ще кілька паралелепіпедів Ейлера:
(275, 252, 240),
(693, 480, 140),
(720, 132, 85),
(792, 231, 160).
Ейлер описав два сімейства таких паралелепіпедів (звідси назва). Втім, повного опису всіх паралелепіпедів Ейлера також немає.
Відомі такі вимоги до ейлерового паралелепіпеда (а значить, і до цілочисельної цеглини):
- Одне ребро ділиться на 4, друге ділиться на 16, третє непарне (якщо, звичайно, він примітивний — тобто, НСД (a, b, c) = 1).
- Одне ребро ділиться на 3 і ще одне — на 9.
- Одне ребро ділиться на 5.
- Одне ребро ділиться на 11.
- Одне ребро ділиться на 19.
- Одне ребро або просторова діагональ діляться на 13.
- Одне ребро, лицьова або просторова діагональ діляться на 17.
- Одне ребро, лицьова або просторова діагональ діляться на 29.
- Одне ребро, лицьова або просторова діагональ діляться на 37.
- Добуток ребер, лицьових і просторової діагоналі має ділитися на 2^8·3^4·5^3·7·11·13·17·19·29·37

Це повідомлення відредагував x3mEn: Oct 22 2013, 09:16

[x3mEn]

Саме так і працює моя програма.
Поясню на прикладі, як відбувається перебір діагоналей.

Перші члени послідовності простих чисел виду 4k+1 наступні:
5, 13, 17, 29, 37, 41...
Беремо перший елемент 5. Це і є перша діагональ.
Друга діагональ - це 5^2, третя - 5^3 і т.д. аж до 5^27 (5^28 вже більше 2^64)
Тепер ступінь 5 обнулюємо, беремо наступне просте - 13. Це наступна діагональ.
Наступна діагональ - 13*5, наступна - 13*5^2 і т.д. аж до 13*5^25.
Далі беремо 13^2 і утворюємо діагональ добутком з усіма ступенями 5, аж до (13^2)*(5^24).

Ну, я думаю зрозуміло.

Проблема полягає тільки у тому, що набір простих чисел виду 4k+1 заздалагідь невідомий і треба вирішити, чи то спочатку організувати пошук простих виду 4k+1, сформувати базу, а потім у завданні для клієнта просто віддавати набори простих чисел, які треба комбінаторно перебрати, аби не змушувати шукати прості числа числа. Чи то залишити за клієнтом задачу пошуку простих чисел виду 4k+1 у заданому діапазоні.

Я особисто схильний до того, щоб клієнти не займалися пошуками простих чисел, а лише перебирали всі їх комбінації.
Як показує моя практика, якщо вже є якийсь, назвемо базовий набір простих, чисел, наприклад (73, 53^2), то для клієнта буде достатньо роботи, аби утворити і перевірити всі комбінації простих чисел виду 4k+1 із множини (5, 13, 17, 29, 37, 41) у всіх різноманітних їх ступенях у комбінації з базовим набором, так, що їх загальний добуток менший за 2^64.

Тому я пропоную завдання для клієнта формувати наступним чином:
(базовий набір) ; (динамічний набір).
Так, наприклад завдання виду
(53^2, 73) ; (5, 13, 17, 29, 37, 41) буде означати, що треба перебрати всі комбінації діагоналей, утворених добутком елементів базового набору (53^2, 73) з усіма можливими комбінаціями елементів динамічного набору (5, 13, 17, 29, 37, 41) в усіх можливих ступенях, таких, що загальний добуток менший за 2^64
За такої постановки задачі клієнти не будуть витрачати час на пошук простих чисел.
Звичайно, що знайти наступне просте число виду 4k+1 не є великою проблемою для клієнта, якщо 4k+1, скажімо, менше за 1 000 000, але 1 000 000 - це тільки 2^20, а що робити, коли просте число буде порядку 2^50 і треба буде знайти наступне просте число? Клієнт вимушений буде витратити годину часу, аби тільки знайти, перевірити на простоту і, між іншим, лише задля того, щоб утворити з ним умовно кажучи пару-трійку комбінацій і впевнитись, що вони не утворюють Ідеального кубоїда. Дуже не ефективне використання ресурсів.

Розмір динамічного діапазону залижить від елементів базового набору. Чим добуток елементів базового набору менший, тим менший має бути набір динамічного набору, адже за маленького добутку елементів базового набору ступенів свободи для динамічного набору більше. І навпаки. коли базовий набір буде рости і наближатися до 2^64, тим менше ступенів свободи у динамічного набору, а значить менша кількість діагоналей які треба перебрати, а отже, щоб завдання не було зовсім коротким, базовий набір для одного завдання буде складатися з великого за кількістю елементів базового набору великих простих чисел виду 4k+1.

Ну, я сподіваюсь ви не позасинали, поки дочитали до звідси.
В дійсності в цьомі проекті буде дуже багато математики, комбінаторики, теорії чисел і таке інше, тому звикайте
Або не читайте і віддайте на потану тим, кому це цікаво.