Perfect Cuboid, Задача про цілочисельний паралелепіпед Налаштування

[x3mEn]

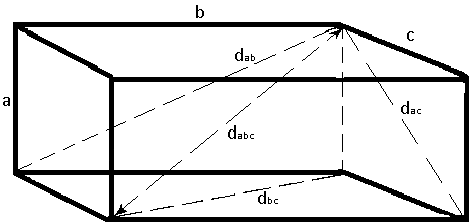Раціональний кубоїд (або цілочисельна цеглина, або ідеальний кубоїд) — прямокутний паралелепіпед,
у якого всі сім основних величин (три ребра, три лицьових діагоналі і просторова діагональ) є цілими числами, є однією з відкритих математичних проблем
Інакше кажучи, раціональний кубоїд — цілочисельне рішення системи діофантових рівнянь.

Досі невідомо, чи існує такий паралелепіпед. Комп'ютерний перебір не знайшов жодної цілочисельної цеглини з ребрами до 10^11.
Втім, знайдено кілька «майже цілочисельних» паралелепіпедів, у яких цілочисельними є всі величини, крім однієї:
— одна з лицевих діагоналей не ціле число.
, — одне з ребер не ціле число.
Велика кількість паралелепіпедів Ейлера (з нецілою просторовою діагоналлю, див. нижче).
Косокутні паралелепіпеди, у яких всі сім величин цілі. При цьому досить одного непрямого кута.
У 2005 році тбіліський студент Лаша Маргішвілі запропонував доведення, що цілочисельний кубоід не існує — однак на 2009 рік робота так і не пройшла перевірку незалежними вченими.

Паралелепіпед Ейлера
Прямокутний паралелепіпед, у якого цілочисельні тільки ребра і лицьові діагоналі, називається ейлеровим.
Найменший з паралелепіпедів Ейлера — (240, 117, 44), з лицьовими діагоналями 267, 244 і 125.
Ще кілька паралелепіпедів Ейлера:
(275, 252, 240),
(693, 480, 140),
(720, 132, 85),
(792, 231, 160).
Ейлер описав два сімейства таких паралелепіпедів (звідси назва). Втім, повного опису всіх паралелепіпедів Ейлера також немає.
Відомі такі вимоги до ейлерового паралелепіпеда (а значить, і до цілочисельної цеглини):
- Одне ребро ділиться на 4, друге ділиться на 16, третє непарне (якщо, звичайно, він примітивний — тобто, НСД (a, b, c) = 1).
- Одне ребро ділиться на 3 і ще одне — на 9.
- Одне ребро ділиться на 5.
- Одне ребро ділиться на 11.
- Одне ребро ділиться на 19.
- Одне ребро або просторова діагональ діляться на 13.
- Одне ребро, лицьова або просторова діагональ діляться на 17.
- Одне ребро, лицьова або просторова діагональ діляться на 29.
- Одне ребро, лицьова або просторова діагональ діляться на 37.
- Добуток ребер, лицьових і просторової діагоналі має ділитися на 2^8·3^4·5^3·7·11·13·17·19·29·37

Це повідомлення відредагував x3mEn: Oct 22 2013, 09:16

[x3mEn]

A1ex01,
якраз збирався написати другу частину.

Загальна формула для представлення добутку суми двох квадратів у вигляді суми двох квадратів наступна:
(a^2+b^2)(x^2+y^2) = a^2*x^2 + a^2*y^2 + b^2*x^2 + b^2*y^2,
додамо і віднімемо 2axby:
(a^2+b^2)(x^2+y^2) = a^2*x^2 + 2axby + b^2*y^2 + a^2*y^2 - 2axby + b^2*x^2 = (ax + by)^2 + (bx - ay)^2 (1)
Запам'ятаємо цю формулу, вона нам ще дуже знадобиться.

а) Якщо число n є сумою двох квадратів, то і число 2n представляється у вигляді суми двох квадратів.
Доведення:
Якщо n = x^2 + y^2, то
(x+y)^2 + (x-y)^2 = x^2 + 2xy + y^2 + x^2 - 2xy + y^2 = 2x^2 + 2y^2 = 2(x^2+y^2) = 2n
Тобто
2n = (x+y)^2 + (x-y)^2
Власне, цю формулу можно отримати і з формули (1), якщо згадати, що 2 = 1^2 + 1^2, тобто в формулі (1) a і b = 1.

Теорема 3 (основна теорема арифметики):
Ціле число розкладається на прості множники одним єдиним способом (з точністю до перестановки множників і асоціативності)
Доведення цієї теореми залишимо за дужками.

Будь-яке число n можна представити у вигляді добутку простих чисел трьох типів: 2^a, p(i)^a(i), q(j)^b(j),
де p(i) - прості числа виду 4k+1, a(i) - ступінь числа p(i)
q(j) - прості числа виду 4k+3, b(j) - ступінь числа q(j).
Нехай Q = П q(j)^b(j)
Тоді, якщо Q не є повним квадратом (а це можливо лише тоді, коли всі b(j) парні), то n не можна розкласти на суму квадратів (критерій Жирара).
Якщо ж Q є повним квадратом, то кількість розкладів n дорівнює кількості розкладів числа П(p(i)^a(i)) на суми квадратів

Теорема 4 (формула Діріхле):
Якщо число n розкладається на суму квадратів, то кількість представлень дорівнює [ (П (a(i)+1) +1) / 2 ] (2)
(Якщо кількість множників рівна 0, то добуток вважається рівним 1. Представлення, що відрізняються порядком доданків, не розрізняються)

Запам'ятайте і цю формулу. Вона нам теж знадобиться для перевірки, що ми правильно розклали число на всі можливі суми квадратів.
Доведення цієї теореми можна знайти у тому ж самому пдф-документі (ст.21)

Основні висновки з цієї теореми: :
1) всі ступені 4k+3 мають бути парними, щоб n мало розклади
2) кількість розкладів n залежить тільки від ступенів 4k+1
3) наявність чи відсутність у розкладі двійки (2) у будь-яких ступенях не впливає ні на "розкладність" n, ні на кількість розкладів

Так от, із Теореми 4 і загальної формули (1) випливає, якщо n - парне і розкладається на суму квадратів m різними способами,
то і число n/2 розкладається на суми квадратів і до того ж теж m різними способами.
При цьому способи розкладу n/2 утворюються із розкладів n одним єдиним способом.
Яким саме - залишаю вам це завдання в якості домашнього завдання. )

Отже, запам'ятаємо цей результат:
Якщо число n має m розкладів на суму квадратів n = x(i)^2 + y(i)^2, то і число 2n має m розкладів, при цьому самі розклади утворюються одним єдиним способом:
2n = (x+y)^2 + (x-y)^2
Цей факт буде використаний пізніше.