Perfect Cuboid, Задача про цілочисельний паралелепіпед Налаштування

[x3mEn]

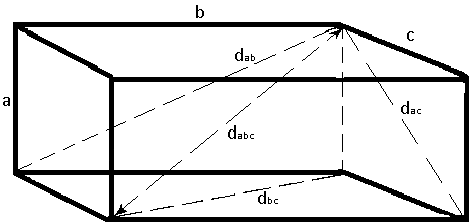Раціональний кубоїд (або цілочисельна цеглина, або ідеальний кубоїд) — прямокутний паралелепіпед,
у якого всі сім основних величин (три ребра, три лицьових діагоналі і просторова діагональ) є цілими числами, є однією з відкритих математичних проблем
Інакше кажучи, раціональний кубоїд — цілочисельне рішення системи діофантових рівнянь.

Досі невідомо, чи існує такий паралелепіпед. Комп'ютерний перебір не знайшов жодної цілочисельної цеглини з ребрами до 10^11.
Втім, знайдено кілька «майже цілочисельних» паралелепіпедів, у яких цілочисельними є всі величини, крім однієї:
— одна з лицевих діагоналей не ціле число.
, — одне з ребер не ціле число.
Велика кількість паралелепіпедів Ейлера (з нецілою просторовою діагоналлю, див. нижче).
Косокутні паралелепіпеди, у яких всі сім величин цілі. При цьому досить одного непрямого кута.
У 2005 році тбіліський студент Лаша Маргішвілі запропонував доведення, що цілочисельний кубоід не існує — однак на 2009 рік робота так і не пройшла перевірку незалежними вченими.

Паралелепіпед Ейлера
Прямокутний паралелепіпед, у якого цілочисельні тільки ребра і лицьові діагоналі, називається ейлеровим.
Найменший з паралелепіпедів Ейлера — (240, 117, 44), з лицьовими діагоналями 267, 244 і 125.
Ще кілька паралелепіпедів Ейлера:
(275, 252, 240),
(693, 480, 140),
(720, 132, 85),
(792, 231, 160).
Ейлер описав два сімейства таких паралелепіпедів (звідси назва). Втім, повного опису всіх паралелепіпедів Ейлера також немає.
Відомі такі вимоги до ейлерового паралелепіпеда (а значить, і до цілочисельної цеглини):
- Одне ребро ділиться на 4, друге ділиться на 16, третє непарне (якщо, звичайно, він примітивний — тобто, НСД (a, b, c) = 1).
- Одне ребро ділиться на 3 і ще одне — на 9.
- Одне ребро ділиться на 5.
- Одне ребро ділиться на 11.
- Одне ребро ділиться на 19.
- Одне ребро або просторова діагональ діляться на 13.
- Одне ребро, лицьова або просторова діагональ діляться на 17.
- Одне ребро, лицьова або просторова діагональ діляться на 29.
- Одне ребро, лицьова або просторова діагональ діляться на 37.
- Добуток ребер, лицьових і просторової діагоналі має ділитися на 2^8·3^4·5^3·7·11·13·17·19·29·37

Це повідомлення відредагував x3mEn: Oct 22 2013, 09:16

[x3mEn]

Далі.
Якщо число n має m розкладів на суму квадратів n = x(i)^2 + y(i)^2, то число 4n теж має m розладів, до того ж самі розклади утворюються із розкладів n ще простіше, аніж для 2n:
4n = 2^2 * n = (2x)^2 + (2y)^2

Давайте тепер повернемося до нашої задачі.
a^2 + b^2 = d^2
a^2 + c^2 = e^2
b^2 + c^2 = f^2
a^2 + f^2 = g^2

Ребра a, b, c мають бути різні, це зрозуміло, тому
для g^2 має існувати як мінімум 3 різні розклади на суми квадратів:
g^2 = a^2 + f^2
g^2 = b^2 + e^2
g^2 = c^2 + d^2

Для того, щоб n = g^2 розкладалося на суму квадратів, потрібно, щоб у розкладі n прості числа 4k+3 були представлені у парних ступенях.
До того ж n має бути повним квадратом, а це можливо тоді і тільки тоді, коли всі прості множники n представлені у парних ступенях.

Тепер доведемо, що діагональ мінімального ідеального кубоїда є непарним числом.
По-перше зазначимо, що якщо ідеальний кубоїд існує, значить їх існує нескінченно багато.
Адже лінійно збільшуючи "габарити" кубоїда ми отримаємо так само ідеальний кубоїд.
Тому задача полягає в пошуку ідеального кубоїда мінімального розміру.

Припустимо, що просторова діагональ g є числом парним.
Тоді, як доведено вище, має розклад на суму квадратів і число (g/2)^2.
І нам відомо, яким саме єдиним чином:
(g/2)^2 = (a/2)^2 + (f/2)^2
(g/2)^2 = (b/2)^2 + (e/2)^2
(g/2)^2 = (c/2)^2 + (d/2)^2
З парності g випливає парність a, b, c, d, e, f
Отже кубоїд з парною просторовою діагоналлю g не є мінімальним.
Висновок: парні просторові діагоналі нас не цікавлять.
А значить шукана g має бути числом непарним.