Привіт Гість ( Вхід | Реєстрація )
| x3mEn |
 Aug 6 2010, 00:01 Aug 6 2010, 00:01
Пост
#1
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
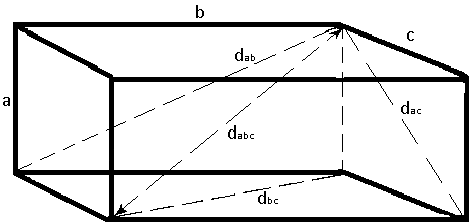 Раціональний кубоїд (або цілочисельна цеглина, або ідеальний кубоїд) — прямокутний паралелепіпед, у якого всі сім основних величин (три ребра, три лицьових діагоналі і просторова діагональ) є цілими числами, є однією з відкритих математичних проблем Інакше кажучи, раціональний кубоїд — цілочисельне рішення системи діофантових рівнянь.  Досі невідомо, чи існує такий паралелепіпед. Комп'ютерний перебір не знайшов жодної цілочисельної цеглини з ребрами до 10^11. Втім, знайдено кілька «майже цілочисельних» паралелепіпедів, у яких цілочисельними є всі величини, крім однієї:  — одна з лицевих діагоналей не ціле число. — одна з лицевих діагоналей не ціле число. , ,  — одне з ребер не ціле число. — одне з ребер не ціле число.Велика кількість паралелепіпедів Ейлера (з нецілою просторовою діагоналлю, див. нижче). Косокутні паралелепіпеди, у яких всі сім величин цілі. При цьому досить одного непрямого кута. У 2005 році тбіліський студент Лаша Маргішвілі запропонував доведення, що цілочисельний кубоід не існує — однак на 2009 рік робота так і не пройшла перевірку незалежними вченими. Паралелепіпед Ейлера Прямокутний паралелепіпед, у якого цілочисельні тільки ребра і лицьові діагоналі, називається ейлеровим. Найменший з паралелепіпедів Ейлера — (240, 117, 44), з лицьовими діагоналями 267, 244 і 125. Ще кілька паралелепіпедів Ейлера: (275, 252, 240), (693, 480, 140), (720, 132, 85), (792, 231, 160). Ейлер описав два сімейства таких паралелепіпедів (звідси назва). Втім, повного опису всіх паралелепіпедів Ейлера також немає. Відомі такі вимоги до ейлерового паралелепіпеда (а значить, і до цілочисельної цеглини): - Одне ребро ділиться на 4, друге ділиться на 16, третє непарне (якщо, звичайно, він примітивний — тобто, НСД (a, b, c) = 1). - Одне ребро ділиться на 3 і ще одне — на 9. - Одне ребро ділиться на 5. - Одне ребро ділиться на 11. - Одне ребро ділиться на 19. - Одне ребро або просторова діагональ діляться на 13. - Одне ребро, лицьова або просторова діагональ діляться на 17. - Одне ребро, лицьова або просторова діагональ діляться на 29. - Одне ребро, лицьова або просторова діагональ діляться на 37. - Добуток ребер, лицьових і просторової діагоналі має ділитися на 2^8·3^4·5^3·7·11·13·17·19·29·37 Це повідомлення відредагував x3mEn: Oct 22 2013, 09:16 --------------------  (Show/Hide) |
  |
Відповідей
| Rilian |
 Aug 6 2010, 00:47 Aug 6 2010, 00:47
Пост
#2
|
 interstellar           Група: Team member Повідомлень: 17 171 З нами з: 22-February 06 З: Торонто Користувач №: 184 Стать: НеСкажу Free-DC_CPID Парк машин: 2 ноути і 4 компа |
я эту задачу уже рассматривал, не зря тестовый боинк висел у нас на поддомене cuboid
потом почитал новости по теме, там уже перебрали немеряное кол-во чисел, и для больших ничего не нашли -------------------- |
| x3mEn |
 Aug 6 2010, 01:16 Aug 6 2010, 01:16
Пост
#3
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
Є одна дуже цікава задача мого дитинства - задача про "цілочисельний паралепіпед".
Прямокутний паралепіпед, в якого є 7 невідомих: 3 ребра, 3 його лицьові діагоналі, 1 просторова діагональ. Задача полягає, чи існує такий паралепіпед, в якого всі 7 вказаних змінних є цілими числами? Задача еквівалента вирішенню системи діафантових рівнянь: a2+b2=d2 a2+c2=e2 b2+c2=f2 b2+e2=g2 Станом на 1988 задача не була вирішена, як і не було доведено, що рішення не існує. Пропоную організувати прямий розумний перебір. Беремо 3 натуральних числа a, b и c, такі, що a < b < c, a+1 <= b <= (a^2-4)/4, b+1 < с <= (a^2-1)/2 Для кожного а організовуємо 2 вкладені цикли: for b = (a + 1) to int((a^2 - 4)/4) if checkab(a, b) <> 0 then d = checkz(a, b) if d <> 0 then for c = (b + 1) to int((a^2 - 1)/2) if checkabc(a, b, c) <> 0 then e = checkz(a, c) if e <> 0 then f = checkz(b, c) if f <>0 then g = checkz(b, e) if g <> 0 then addresult(a, b, c, d, e, f, g) endif endif endif endif endfor endif endif endfor В функції checkab(a, b) перевіряємо, що a і b не є одночасно непарними. В функції checkabc(a, b, c) перевіряємо, що: 1. серед a, b і c тільки одне число непарне. 2. одне з чисел ділить на 4, а одне з інших - на 16 3. одне з чисел ділить на 3, а одне з інших - на 9 4. одне з чисел ділить на 5 5. одне з чисел ділить на 7 6. одне з чисел ділить на 9 7. одне з чисел ділить на 11 8. одне з чисел ділить на 19 В функції checkz(x, y) перевіряємо, чи існує натуральне z, таке, що x2+y2=z2. Якщо не існує, повертаємо 0. Існує - звісно повертаємо z. Тут є декілька думок: Перша - перевірка останньої цифри суми квадратів. Оскільки остання цифра квадрату може бути: 1 - 1 2 - 4 3 - 9 4 - 6 5 - 5 6 - 6 7 - 9 8 - 4 9 - 1 0 - 0 Отже квадрат може закінчуватись тільки на (0, 1, 4, 5, 6, 9), а сума квадратів може приймати значення з імовірностями: 0 - 16,67% 1 - 11,11% 2 - 5,56% 3 - 5,56% 4 - 11,11% 5 - 16,67% 6 - 11,11% 7 - 5,56% 8 - 5,56% 9 - 11,11% Отже, ще до будь-яких піднесень до квадратів можна одразу відкинути 2/9 всіх пар чисел. Ще один випадок, що можна швиденько відкинути: якщо остання цифра суми квадратів закінчується на 0, шуканий квадрат має закінчуватись на 00. Задля цієї перевірки достатньо перевірити: k = x rem 100 l = y rem 100 тобто k і l - числа, складені з двох останніх цифр x та y відповідно. Тоді треба перевірити, що (k^2 + 2k + l^2 + 2l) rem 100 = 0 Ну а далі треба шукати швидкі методи пошуку натуральних коренів. Поки що все. P.S.: Процедура addresult() зберігає результат і виплачує премію в 1000 дол. P.P.S.: Почитав пости назад у часі... ідея з пошуком "ідеального кубоіда" вже була, тільки що brute force без особливих оптимізацій. Тому вибачаюсь за повтор. Витирати посилання не буду, оскільки приклав багато зусиль, щоб все викласти, що в голові було. P.P.P.S: якщо є обчислювальні обмеження з точним обрахунком квадрату числа (можу припустити, що так воно і є), можу запропонувати організацію вкладених циклів в оберненому порядку від більшого числа до меншого. Тобто спочатку фіксуємо найбільше з ребер c, потім організовуємо цикл вниз від (с-1) до int(sqrt(4c+4)) для числа b, ну а потім цикл вниз від (b-1) до int(sqrt(2c+1)) для найменшого з ребер a. Ну а все інше - як викладено вище. На вхід подається 2 числа, m і n: m <= c <= n for c = m to n for b = (с - 1) downto int(sqrt(4c + 4)) if checkab(b, c) <> 0 then f = checkz(b, c) if f <> 0 then for a = (b - 1) downto int(sqrt(2c+1)) if checkabc(a, b, c) <> 0 then d = checkz(a, b) if d <> 0 then e = checkz(a, c) if e <>0 then g = checkz(b, e) if g <> 0 then addresult(a, b, c, d, e, f, g) endif endif endif endif endfor endif endif endfor endfor Числа m і n визначають, як вся задача розрізається на окремі завдання. Вартість завдання можна визначати, наприклад: 1. за кількістю заходів в checkz 2. за кількістю нетривіальних перевірок в середині checkz (алгоритм якої ще треба придумати). 3. за кількістю заходів в checkab 4. за кількістю заходів в checkabc Всі 4 числа мають різну вагу, тому що складність виконання різна. Валідність розрахунку можна визначати теж за цим показником. я эту задачу уже рассматривал, не зря тестовый боинк висел у нас на поддомене cuboid потом почитал новости по теме, там уже перебрали немеряное кол-во чисел, и для больших ничего не нашли А в мене з дитинства залишилась віра, що, якшо знайшли майже ідеальний паралелепіпед (6 з 7 - натуральні), то має бути і повністю ідеальний цеглоїд. --------------------  (Show/Hide) |
| x3mEn |
 Aug 28 2010, 19:44 Aug 28 2010, 19:44
Пост
#4
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
Ситуація така: я задачу не залишив, за останній місяць перечитав достатньо багато літератури з тематики "ідеального кубоїда"
і врешті написав на Delphi 7 LE тестову програму. Ось основна література, на якій базується мій "розумний" перебір: 29 гипотеза Альшина Суммы квадратов и целые гауссовы числа На Вікіпедії вказано, що якщо такий кубоїд існує, найменше ребро має бути більшим за 100млн. 100млн. - це, очевидь, обмеження 32-біт. Тому задача дуже амбітна: перебрати всі підходящі просторові діагоналі для всіх 64-бітних цілих чисел і або таки знайти кубоїд, або довести, що його не існує і серед 64-бітних цілих чисел. Реально це, чи ні - ви самі можете оцінити, виходячи із швидкості перебору на одному ядрі CPU (див. вклад.) Алгоритм пошуку дуже відрізняється від того, що я описав навіть місяць назад. Якщо коротко: я перейшов від перебору ребер до перебору просторових діагоналей. Просторова діагональ може бути тільки числом, що розкладається на прості числа виду 4k+1. Наступна задача - написати GPU-аналог. Виходячи з того, яка швидкість перебору з використанням cuda-клієнта для Collatz Conjecture, мені здається, що на GPU подібні перебори набагато ефективніше працюватимуть. Якщо є специ, що мають досвід роботи з CUDA SDK, відгукніться, будь ласка. Приєднані файл(и)  pcuboid.zip ( 285.04Кб )
Кількість викачувань: 1450
pcuboid.zip ( 285.04Кб )
Кількість викачувань: 1450--------------------  (Show/Hide) |
Повідомлення у даній Темі
 x3mEn Perfect Cuboid Aug 6 2010, 00:01
x3mEn Perfect Cuboid Aug 6 2010, 00:01
 molo Дякую, x3mEn
Хороша робота!
Тільки ще би мале... Aug 30 2010, 07:06
molo Дякую, x3mEn
Хороша робота!
Тільки ще би мале... Aug 30 2010, 07:06

 x3mEn
Дякую, x3mEn
Хороша робота!
Тільки ще би мал... Aug 30 2010, 10:46
x3mEn
Дякую, x3mEn
Хороша робота!
Тільки ще би мал... Aug 30 2010, 10:46
 x3mEn Нова версія тестової програми.
Зміни:
+ Нова стат... Sep 1 2010, 11:47
x3mEn Нова версія тестової програми.
Зміни:
+ Нова стат... Sep 1 2010, 11:47
 molo Привіт Усім!
Дякуючи хорошим ідеям про ‘наш ... Jan 28 2011, 08:06
molo Привіт Усім!
Дякуючи хорошим ідеям про ‘наш ... Jan 28 2011, 08:06
 re_SET molo, Насколько сложная задача в плане выч. мощнос... Jan 28 2011, 10:02
re_SET molo, Насколько сложная задача в плане выч. мощнос... Jan 28 2011, 10:02

 molo
[b]molo, Насколько сложная задача в плане выч. мо... Jan 28 2011, 11:41
molo
[b]molo, Насколько сложная задача в плане выч. мо... Jan 28 2011, 11:41

 x3mEn
[quote name='re_SET' post='72969' date='Jan 28 20... Jan 28 2011, 19:31
x3mEn
[quote name='re_SET' post='72969' date='Jan 28 20... Jan 28 2011, 19:31

 molo
Хто візьметься зробити хоча б пункт #1, порахув... Jan 28 2011, 20:48
molo
Хто візьметься зробити хоча б пункт #1, порахув... Jan 28 2011, 20:48
 Rilian molo, мне кажется я видел в интернете инфу что как... Jan 28 2011, 12:43
Rilian molo, мне кажется я видел в интернете инфу что как... Jan 28 2011, 12:43

 molo
molo, мне кажется я видел в интернете инфу что ка... Jan 28 2011, 19:22
molo
molo, мне кажется я видел в интернете инфу что ка... Jan 28 2011, 19:22
 x3mEn Саме так і працює моя програма.
Поясню на прикладі... Jan 28 2011, 22:35
x3mEn Саме так і працює моя програма.
Поясню на прикладі... Jan 28 2011, 22:35
 Death список простых чисел примерно до миллиарда давно и... Jan 28 2011, 22:59
Death список простых чисел примерно до миллиарда давно и... Jan 28 2011, 22:59

 x3mEn
roughly 2х10^21 below 10^23
(2^64)/(5^2) = ~ 7.3... Jan 28 2011, 23:17
x3mEn
roughly 2х10^21 below 10^23
(2^64)/(5^2) = ~ 7.3... Jan 28 2011, 23:17
 x3mEn Я сподіваюсь, що після усього мною сказаного зрозу... Jan 28 2011, 23:02
x3mEn Я сподіваюсь, що після усього мною сказаного зрозу... Jan 28 2011, 23:02
 x3mEn До речі, простих чисел менших за 2^32 якщо теж бли... Jan 28 2011, 23:36
x3mEn До речі, простих чисел менших за 2^32 якщо теж бли... Jan 28 2011, 23:36
 Death не, там дальше их количество уменьшается.
пи(х) не... Jan 29 2011, 00:00
Death не, там дальше их количество уменьшается.
пи(х) не... Jan 29 2011, 00:00  |
1 Користувачів переглядають дану тему (1 Гостей і 0 Прихованих Користувачів)
0 Користувачів:

|
Lo-Fi Версія | Поточний час: 6th February 2026 - 21:22 |



















