Привіт Гість ( Вхід | Реєстрація )
| x3mEn |
 Aug 6 2010, 00:01 Aug 6 2010, 00:01
Пост
#1
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
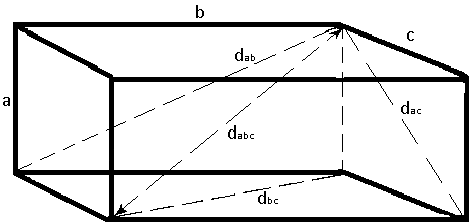 Раціональний кубоїд (або цілочисельна цеглина, або ідеальний кубоїд) — прямокутний паралелепіпед, у якого всі сім основних величин (три ребра, три лицьових діагоналі і просторова діагональ) є цілими числами, є однією з відкритих математичних проблем Інакше кажучи, раціональний кубоїд — цілочисельне рішення системи діофантових рівнянь.  Досі невідомо, чи існує такий паралелепіпед. Комп'ютерний перебір не знайшов жодної цілочисельної цеглини з ребрами до 10^11. Втім, знайдено кілька «майже цілочисельних» паралелепіпедів, у яких цілочисельними є всі величини, крім однієї:  — одна з лицевих діагоналей не ціле число. — одна з лицевих діагоналей не ціле число. , ,  — одне з ребер не ціле число. — одне з ребер не ціле число.Велика кількість паралелепіпедів Ейлера (з нецілою просторовою діагоналлю, див. нижче). Косокутні паралелепіпеди, у яких всі сім величин цілі. При цьому досить одного непрямого кута. У 2005 році тбіліський студент Лаша Маргішвілі запропонував доведення, що цілочисельний кубоід не існує — однак на 2009 рік робота так і не пройшла перевірку незалежними вченими. Паралелепіпед Ейлера Прямокутний паралелепіпед, у якого цілочисельні тільки ребра і лицьові діагоналі, називається ейлеровим. Найменший з паралелепіпедів Ейлера — (240, 117, 44), з лицьовими діагоналями 267, 244 і 125. Ще кілька паралелепіпедів Ейлера: (275, 252, 240), (693, 480, 140), (720, 132, 85), (792, 231, 160). Ейлер описав два сімейства таких паралелепіпедів (звідси назва). Втім, повного опису всіх паралелепіпедів Ейлера також немає. Відомі такі вимоги до ейлерового паралелепіпеда (а значить, і до цілочисельної цеглини): - Одне ребро ділиться на 4, друге ділиться на 16, третє непарне (якщо, звичайно, він примітивний — тобто, НСД (a, b, c) = 1). - Одне ребро ділиться на 3 і ще одне — на 9. - Одне ребро ділиться на 5. - Одне ребро ділиться на 11. - Одне ребро ділиться на 19. - Одне ребро або просторова діагональ діляться на 13. - Одне ребро, лицьова або просторова діагональ діляться на 17. - Одне ребро, лицьова або просторова діагональ діляться на 29. - Одне ребро, лицьова або просторова діагональ діляться на 37. - Добуток ребер, лицьових і просторової діагоналі має ділитися на 2^8·3^4·5^3·7·11·13·17·19·29·37 Це повідомлення відредагував x3mEn: Oct 22 2013, 09:16 --------------------  (Show/Hide) |
  |
Відповідей(1 - 14)
| Rilian |
 Aug 6 2010, 00:47 Aug 6 2010, 00:47
Пост
#2
|
 interstellar           Група: Team member Повідомлень: 17 166 З нами з: 22-February 06 З: Торонто Користувач №: 184 Стать: НеСкажу Free-DC_CPID Парк машин: 2 ноути і 4 компа |
я эту задачу уже рассматривал, не зря тестовый боинк висел у нас на поддомене cuboid
потом почитал новости по теме, там уже перебрали немеряное кол-во чисел, и для больших ничего не нашли -------------------- |
| x3mEn |
 Aug 6 2010, 01:16 Aug 6 2010, 01:16
Пост
#3
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
Є одна дуже цікава задача мого дитинства - задача про "цілочисельний паралепіпед".
Прямокутний паралепіпед, в якого є 7 невідомих: 3 ребра, 3 його лицьові діагоналі, 1 просторова діагональ. Задача полягає, чи існує такий паралепіпед, в якого всі 7 вказаних змінних є цілими числами? Задача еквівалента вирішенню системи діафантових рівнянь: a2+b2=d2 a2+c2=e2 b2+c2=f2 b2+e2=g2 Станом на 1988 задача не була вирішена, як і не було доведено, що рішення не існує. Пропоную організувати прямий розумний перебір. Беремо 3 натуральних числа a, b и c, такі, що a < b < c, a+1 <= b <= (a^2-4)/4, b+1 < с <= (a^2-1)/2 Для кожного а організовуємо 2 вкладені цикли: for b = (a + 1) to int((a^2 - 4)/4) if checkab(a, b) <> 0 then d = checkz(a, b) if d <> 0 then for c = (b + 1) to int((a^2 - 1)/2) if checkabc(a, b, c) <> 0 then e = checkz(a, c) if e <> 0 then f = checkz(b, c) if f <>0 then g = checkz(b, e) if g <> 0 then addresult(a, b, c, d, e, f, g) endif endif endif endif endfor endif endif endfor В функції checkab(a, b) перевіряємо, що a і b не є одночасно непарними. В функції checkabc(a, b, c) перевіряємо, що: 1. серед a, b і c тільки одне число непарне. 2. одне з чисел ділить на 4, а одне з інших - на 16 3. одне з чисел ділить на 3, а одне з інших - на 9 4. одне з чисел ділить на 5 5. одне з чисел ділить на 7 6. одне з чисел ділить на 9 7. одне з чисел ділить на 11 8. одне з чисел ділить на 19 В функції checkz(x, y) перевіряємо, чи існує натуральне z, таке, що x2+y2=z2. Якщо не існує, повертаємо 0. Існує - звісно повертаємо z. Тут є декілька думок: Перша - перевірка останньої цифри суми квадратів. Оскільки остання цифра квадрату може бути: 1 - 1 2 - 4 3 - 9 4 - 6 5 - 5 6 - 6 7 - 9 8 - 4 9 - 1 0 - 0 Отже квадрат може закінчуватись тільки на (0, 1, 4, 5, 6, 9), а сума квадратів може приймати значення з імовірностями: 0 - 16,67% 1 - 11,11% 2 - 5,56% 3 - 5,56% 4 - 11,11% 5 - 16,67% 6 - 11,11% 7 - 5,56% 8 - 5,56% 9 - 11,11% Отже, ще до будь-яких піднесень до квадратів можна одразу відкинути 2/9 всіх пар чисел. Ще один випадок, що можна швиденько відкинути: якщо остання цифра суми квадратів закінчується на 0, шуканий квадрат має закінчуватись на 00. Задля цієї перевірки достатньо перевірити: k = x rem 100 l = y rem 100 тобто k і l - числа, складені з двох останніх цифр x та y відповідно. Тоді треба перевірити, що (k^2 + 2k + l^2 + 2l) rem 100 = 0 Ну а далі треба шукати швидкі методи пошуку натуральних коренів. Поки що все. P.S.: Процедура addresult() зберігає результат і виплачує премію в 1000 дол. P.P.S.: Почитав пости назад у часі... ідея з пошуком "ідеального кубоіда" вже була, тільки що brute force без особливих оптимізацій. Тому вибачаюсь за повтор. Витирати посилання не буду, оскільки приклав багато зусиль, щоб все викласти, що в голові було. P.P.P.S: якщо є обчислювальні обмеження з точним обрахунком квадрату числа (можу припустити, що так воно і є), можу запропонувати організацію вкладених циклів в оберненому порядку від більшого числа до меншого. Тобто спочатку фіксуємо найбільше з ребер c, потім організовуємо цикл вниз від (с-1) до int(sqrt(4c+4)) для числа b, ну а потім цикл вниз від (b-1) до int(sqrt(2c+1)) для найменшого з ребер a. Ну а все інше - як викладено вище. На вхід подається 2 числа, m і n: m <= c <= n for c = m to n for b = (с - 1) downto int(sqrt(4c + 4)) if checkab(b, c) <> 0 then f = checkz(b, c) if f <> 0 then for a = (b - 1) downto int(sqrt(2c+1)) if checkabc(a, b, c) <> 0 then d = checkz(a, b) if d <> 0 then e = checkz(a, c) if e <>0 then g = checkz(b, e) if g <> 0 then addresult(a, b, c, d, e, f, g) endif endif endif endif endfor endif endif endfor endfor Числа m і n визначають, як вся задача розрізається на окремі завдання. Вартість завдання можна визначати, наприклад: 1. за кількістю заходів в checkz 2. за кількістю нетривіальних перевірок в середині checkz (алгоритм якої ще треба придумати). 3. за кількістю заходів в checkab 4. за кількістю заходів в checkabc Всі 4 числа мають різну вагу, тому що складність виконання різна. Валідність розрахунку можна визначати теж за цим показником. я эту задачу уже рассматривал, не зря тестовый боинк висел у нас на поддомене cuboid потом почитал новости по теме, там уже перебрали немеряное кол-во чисел, и для больших ничего не нашли А в мене з дитинства залишилась віра, що, якшо знайшли майже ідеальний паралелепіпед (6 з 7 - натуральні), то має бути і повністю ідеальний цеглоїд. --------------------  (Show/Hide) |
| x3mEn |
 Aug 28 2010, 19:44 Aug 28 2010, 19:44
Пост
#4
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
Ситуація така: я задачу не залишив, за останній місяць перечитав достатньо багато літератури з тематики "ідеального кубоїда"
і врешті написав на Delphi 7 LE тестову програму. Ось основна література, на якій базується мій "розумний" перебір: 29 гипотеза Альшина Суммы квадратов и целые гауссовы числа На Вікіпедії вказано, що якщо такий кубоїд існує, найменше ребро має бути більшим за 100млн. 100млн. - це, очевидь, обмеження 32-біт. Тому задача дуже амбітна: перебрати всі підходящі просторові діагоналі для всіх 64-бітних цілих чисел і або таки знайти кубоїд, або довести, що його не існує і серед 64-бітних цілих чисел. Реально це, чи ні - ви самі можете оцінити, виходячи із швидкості перебору на одному ядрі CPU (див. вклад.) Алгоритм пошуку дуже відрізняється від того, що я описав навіть місяць назад. Якщо коротко: я перейшов від перебору ребер до перебору просторових діагоналей. Просторова діагональ може бути тільки числом, що розкладається на прості числа виду 4k+1. Наступна задача - написати GPU-аналог. Виходячи з того, яка швидкість перебору з використанням cuda-клієнта для Collatz Conjecture, мені здається, що на GPU подібні перебори набагато ефективніше працюватимуть. Якщо є специ, що мають досвід роботи з CUDA SDK, відгукніться, будь ласка. Приєднані файл(и)  pcuboid.zip ( 285.04Кб )
Кількість викачувань: 1447
pcuboid.zip ( 285.04Кб )
Кількість викачувань: 1447--------------------  (Show/Hide) |
| molo |
 Aug 30 2010, 07:06 Aug 30 2010, 07:06
Пост
#5
|
 Трохи обжився   Група: Trusted Members Повідомлень: 23 З нами з: 21-January 09 Користувач №: 906 Стать: Чол |
Дякую, x3mEn
Хороша робота! Тільки ще би маленького мануала для усіх Щодо GPU версії, то звичайно потрібно, але почати можна би було і зі звичайної CPU версії для Windows OS. Потім неодмінно покрити інші. Клієнтська частина виглядає не дуже складною (простий перебір, щоб 100% перевірити) + комунікація з серверною частиною (відсилка результатів, отримання задачі, оновлення клієнта) - для початку, здається досить. Я так, розумію, питання щодо серверної частини досі відкрите - чи будемо використовувати Boinc чи інший аналог (точно і не знаю чи щось нове з'явилось).Іншим варіантом є розробка своєї серверної частини (Java або .NET, maybe PHP + database MySQL). Чим раніше ми би випустили робочу версію (клієнт-сервер + реєстрація користувачів + статистика) тим потенційно більше би людей ми могли б найти для проекту. Бо більшість серйозних людей навіть не звернуть увагу, коли у нас крім балачок нічого ще нема. Як тільки буде визначено з серверною частиною, то, гадаю, ми могли б шукати бажаючих допомогти і формувати активну частину проекту (внутрішні обговорення, SVN, wiki, TODOs etc.) -------------------- |
| x3mEn |
 Aug 30 2010, 10:46 Aug 30 2010, 10:46
Пост
#6
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
Дякую, x3mEn Хороша робота! Тільки ще би маленького мануала для усіх Мануал до тестової програми? Ну, по-перше перебір ведеться серед діагоналей, що утворюються різними комбінаціями добутків простих чисел виду 4k+1 у різних ступенях. У віконці Current position можна побачити поточну позицію перебору. У таблиці - фактори і їх ступені, в полі Diagonal - відповідне значення діагоналі. Squares - кількість різних розкладань числа Diagonal на суму двох квадратів. До речі, перевірити розкладання можна, якщо поставити галочку Save squares to .txt files, тоді в директорії, звідки зпускалась програма, будуть створюватись файли з назвою = значенню Diagonal, а всередині через кому будуть перелічені всі пари розкладів. Кількість розкладів можна розрахувати за відомою формулою. Власне, я дуже втішаюсь, що кількість розкладів, що я отримую за алгоритмом, збігається із значенням за формулою. Наприклад: 5**7 13**1 17**2 29**2 37**2 41**1 53**1 Тобто діагональ = 734328519856953125 Кількість розкладів: [((2*7+1)(2*1+1)(2*2+1)(2*2+1)(2*2+1)(2*1+1)(2*1+1)+1)/2] = [(15*3*5*5*5*3*3+1)/2] = 25313 Для кожної діагоналі на основі її розкладу на суму квадратів відбувається пошук усіх інших 6 вимірів (3 ребра, 3 лицьові діагоналі). Розділ Last Checked Candidate власне створений для того, щоб візулізувати пошук. Для кожної діагоналі кількість переборів має порядок Q^2, де Q - кількість розкладів. У найгіршому випадку = (Q^2)/2, у найкращому - 0. Власне, це найкращий порядок, якого я досяг. За рахунок певних оптимізацій, таких як, наприклад: - попередня перевірка, що 2 ребра не можуть бути одночасно непарними числами, - для обраної лицьової діагоналі F перебір одного з ребер тільки до значення sqrt(F) і таке інше кількість переборів ще скорочується, може десь в 2-3 рази. Settings: встановлення початкової і кінцевої позицій перебору. Manual - вручну, інакше - з файлу. Метод вручну обмежується встановленням одного значення фактору і його ступеню. Через файл початкову і кінцеву позицію можна встановити точніше. У будь-якому випадку під час обрахунку у файлі зберігається остання позиція. Власне, за змовченням встановлено метод "Через файл", разом з exe я додав task64.txt з останною позицією, до якої я дорахував на той момент. Якщо обрати метод Manual, тоді файл буде створено самостійно, пізніше за великого бажання можна самостійно змінити початкові і кінцеві позиції через будь-який текстовий редактор. Параметр "кінцева позиція" є необов'язковим, якщо спочатку не вказано, перебір буде тривати, поки не перебере все до кінця. Refresh Frequence (sec) я створив для того випадку, якщо перебір відбувається вже надто швидко і візуалізація гальмує сам перебір. Це було корисно, наприклад, коли я створив версію програми, що відтворює пошук лише серед 32 бітних цілих. Тоді перебір відбувається аж надто швидко. Якщо цікаво, можу скомпілювати 32 бітну версію і викласти сюди. В мене є враження, що 32-бітний перебір взагалі можна зробити силами однієї машини. В мене, правда, є певні сумніви щодо швидкості пошуку простих чисел у високих діапазонах чисел, можливо це свого часу стане серйозним гальмом. Але, принаймні за пігодинки в 32-бітній версії я перебрав всі варіанти факторів аж десь до 70000. Для 32 біт переломним є число 46000, після чого кількість варіантів розкладів тільки падає. А основне гальмо в цьому переборі це не абсолютне значення діагоналі, а кількість розкладів цього числа на суми квадратів. В розділі Statistics показується загальна статистика процесу від початку запуску. Найцікавішими є такі значення: Diagonals checked - кількість перебраних діагоналей Avg Time per G (sec) - середня тривалість перевірки однієї діагоналі Avg Squares per G - середня кількість розкладів діагоналі на суму двох квадратів --------------------  (Show/Hide) |
| x3mEn |
 Sep 1 2010, 11:47 Sep 1 2010, 11:47
Пост
#7
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
Нова версія тестової програми.
Зміни: + Нова статистика, підраховується кількість циклів, ASPG / AGPS - Average seconds per G (diagonal) / Average G (diagonals) per second + Змінено формат збереження тестових завдань, тепер у вигляді Ini файла. За рахунок цього дискові опреації відбуваються за таймером. + Додано збереження проміжного результату статистики (дата початку, тривалість, кількість оброблених діагоналей та ін.) + Пофіксені баги, які могли б "вістрилити" на числах більших за 32 біти + Додано кнопку Reset, аби можна було перервати виконання з обнуленням всіх даних + Змінено логіку визначення кінця завдання. Тепер, якщо вказано, що Finish position, припустимо, 53**1, це значить, що 53**1 буде останнім числом завдання У самому алгоритмі, нажаль, ніяких змін не відбулося. Останнім часом не можу придумати, як ще можна було б зменшити кількість переборів. Вибачте, що викладаю ехе-шник. По-перше не у всіх є Delphi, щоб відкомпілювати, а по-друге, сам алгоритм певним чином складає для мене певну цінність. Я поділюся сорсами тільки якщо знайду того, хто допоможе написати або GPU аналог, або клієнта і сервер, нехай навіть для CPU. Приєднані файл(и)  pcuboid64.zip ( 290.08Кб )
Кількість викачувань: 1430
pcuboid64.zip ( 290.08Кб )
Кількість викачувань: 1430--------------------  (Show/Hide) |
| molo |
 Jan 28 2011, 08:06 Jan 28 2011, 08:06
Пост
#8
|
 Трохи обжився   Група: Trusted Members Повідомлень: 23 З нами з: 21-January 09 Користувач №: 906 Стать: Чол |
Привіт Усім!
Дякуючи хорошим ідеям про ‘наш проект’ - раді повідомити, про початок розробки проекту по пошуку ідеального паралелепіпеда - http://perfectcuboid.com/ Якщо є бажання і час - ласкаво просимо до проекту. Роботи вистачить на усіх Короткий список активностей: 1. Розробка/обговорення алгоритму обчислення 2. Тестування 3. Веб дизайн 4. Адмінування 5. Підтримка сайту 6. Розробка клієнтської частини 7. Розробка серверної частини 8. … Контакти: http://perfectcuboid.com/contact-us team@perfectcuboid.com Першочергові кроки: 1. Початкова інфраструктура серверної частини – в процесі 2. Фіналізувати початковий API для комунікації серверної і клієнтської частини – в процесі 3. Розробка клієнтської частини для Windows Якщо адміністрація distributed.org.ua дозволить – раді продовжити обговорення в даній темі, або новоствореній темі. -------------------- |
| re_SET |
 Jan 28 2011, 10:02 Jan 28 2011, 10:02
Пост
#9
|
 кранчер зі стажем       Група: Trusted Members Повідомлень: 455 З нами з: 26-January 09 З: Волинська обл., смт. Любешів Користувач №: 911 Стать: Чол Парк машин: 1х Athlon X2 BE2300 (2.2 Ghz) 1x C2D E8200 1x C2D E2180 (2.34 Ghz) 1x C2D E2160 1x C2D E5200 (2.9 Ghz) 9x C2D E6500 (Up 3.24 Ghz) 1x C2Q Q8300 (Up 3 Ghz) |
molo, Насколько сложная задача в плане выч. мощностей?
-------------------- Нельзя попасть в Рай одной религии, не попав при этом в Ад всех остальных...
           (Show/Hide) |
| molo |
 Jan 28 2011, 11:41 Jan 28 2011, 11:41
Пост
#10
|
 Трохи обжився   Група: Trusted Members Повідомлень: 23 З нами з: 21-January 09 Користувач №: 906 Стать: Чол |
molo, Насколько сложная задача в плане выч. мощностей? Хороше питання, re_SET! Передусім об’єм обрахунків буде залежати лід алгоритму. x3mEn уже зробив певні дослідження в цьому напрямку. Пригадую я вже робив заміри на десктопному процесорі (див. вище по темі) Повторивши результати: 1.6GHz processor - 1 ядро (laptop) 10^9 комбінацій ~ 5хв – простий перебір Щоб обрахувати кубоід з 10^6 ( 1-1,000,000): 10^6 * 10^6 * 10^6 = 10^18 комбінацій 10^18 комбінацій / (10^9 комб/5хв) = 10^9 циклів по 5хв = 5*10^9 хв = 83,333,333 год = 3,472,222 доби = 9,512 роки Переведемо на 1GHz: Щоб обрахувати кубоід з 10^6 на 1GHz (10^18 комбінацій): 9,512 * 1.6 = 15,219 роки Щоб обрахувати кубоід з 10^11 на 1GHz (10^33 комбінацій) - повторити теперішні обрахунки: 10^33 / 10^18 = 10^15 циклів по 15,219 роки 10^15 * 15,219 роки ~ 15 * 10^15 років Так як навіть зараз процесори мають більші потужності ~ 2*2.5 = 5GHz. Не кажучи про 6-ти ядерні від AMD – 3.5GHz * 6core = 21GHz. Тому з часом швидкість обрахунків буде тільки зростати в рази. Основною складовою буде, як завжди, в розподільних обчисленнях, буде кількість учасників. Виглядає досить амбітно і довготривало. -------------------- |
| Rilian |
 Jan 28 2011, 12:43 Jan 28 2011, 12:43
Пост
#11
|
 interstellar           Група: Team member Повідомлень: 17 166 З нами з: 22-February 06 З: Торонто Користувач №: 184 Стать: НеСкажу Free-DC_CPID Парк машин: 2 ноути і 4 компа |
molo, мне кажется я видел в интернете инфу что какие-то китайцы вычислили до 10^18 все кубоиды и идеального не нашли...
-------------------- |
| molo |
 Jan 28 2011, 19:22 Jan 28 2011, 19:22
Пост
#12
|
 Трохи обжився   Група: Trusted Members Повідомлень: 23 З нами з: 21-January 09 Користувач №: 906 Стать: Чол |
molo, мне кажется я видел в интернете инфу что какие-то китайцы вычислили до 10^18 все кубоиды и идеального не нашли... Тоді хочеться вірити, що початкові підрахунки в мільярди років не зовсім вірні і ми зможемо обрахувати все значно швидше Основна ідея проекту - відкритість результатів, доступних 24/7. Отже кожен зможе слідкувати за статусом. -------------------- |
| x3mEn |
 Jan 28 2011, 19:31 Jan 28 2011, 19:31
Пост
#13
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
molo, Насколько сложная задача в плане выч. мощностей? Щоб обрахувати кубоід з 10^6 ( 1-1,000,000): 10^6 * 10^6 * 10^6 = 10^18 комбінацій 10^18 комбінацій / (10^9 комб/5хв) = 10^9 циклів по 5хв = 5*10^9 хв = 83,333,333 год = 3,472,222 доби = 9,512 роки В дійсності і кількість варіантів і оцінка тривалості зовсім інші. За моїм алгоритмов задля того, щоб підрахувати кількість варіантів, які треба перебрати, треба зробити наступне: 1) знайти всі прості числа виду 4k+1 в діапазоні від 5 до (2^64)/(5^2) (якщо треба, можу пояснити, чому саме до цього числа) 2) із всіх цих простих чисел утворити всі їх комбінації такі, що П p(i)^k(p) < 2^64, де p(i) - просте число, k(p) - ступінь, до якої підноситься це просте число. Це ми отримаємо кількість всіх діагоналей-кандидатів. Діагональ-кандидат дорівнює, відповідно П p(i)^k(p) Потім для кожної діагоналі треба знайти всі розклади на суму квадратів. Кількість таких розкладів вираховується за формулою П (k(p)+1) Час перевірки однієї діагоналі залежить від кількості різних розкладів приблизно у кубічній залежності. Так от щоб хоча б приблизно підрахувати час повного перебору, це треба вирахувати суму кубів по всім діагоналям-кандидатам і поділити на середню швидкість перебору кандидатів. Хто візьметься зробити хоча б пункт #1, порахувати кількість простих чисел виду 4k+1 в діапазоні від 5 до (2^64)(5^2) ? Щоб зрозуміти, цю всю масу простих чисел реально зібрати на одній машині для нарізки завдань, чи для цього ще треба буде організувати підпроект? --------------------  (Show/Hide) |
| molo |
 Jan 28 2011, 20:48 Jan 28 2011, 20:48
Пост
#14
|
 Трохи обжився   Група: Trusted Members Повідомлень: 23 З нами з: 21-January 09 Користувач №: 906 Стать: Чол |
Хто візьметься зробити хоча б пункт #1, порахувати кількість простих чисел виду 4k+1 в діапазоні від 5 до (2^64)/5/13 ? Щоб зрозуміти, цю всю масу простих чисел реально зібрати на одній машині для нарізки завдань, чи для цього ще треба буде організувати підпроект? Це може бути першою стадією того ж проекту. З іншого боку підбір діагоналей може бути здійнений на тому ж клієнті. Для прикладу - пакет 100k-200k спочатку клієнт перебирає діагоналі в заданому діапазоні, а потім веде розрахунки по вибраним діагонаям. -------------------- |
| x3mEn |
 Jan 28 2011, 22:35 Jan 28 2011, 22:35
Пост
#15
|
 snow catcher          Група: Trusted Members Повідомлень: 2 213 З нами з: 4-August 07 Користувач №: 563 Стать: Чол Free-DC_CPID |
Саме так і працює моя програма.
Поясню на прикладі, як відбувається перебір діагоналей. Перші члени послідовності простих чисел виду 4k+1 наступні: 5, 13, 17, 29, 37, 41... Беремо перший елемент 5. Це і є перша діагональ. Друга діагональ - це 5^2, третя - 5^3 і т.д. аж до 5^27 (5^28 вже більше 2^64) Тепер ступінь 5 обнулюємо, беремо наступне просте - 13. Це наступна діагональ. Наступна діагональ - 13*5, наступна - 13*5^2 і т.д. аж до 13*5^25. Далі беремо 13^2 і утворюємо діагональ добутком з усіма ступенями 5, аж до (13^2)*(5^24). Ну, я думаю зрозуміло. Проблема полягає тільки у тому, що набір простих чисел виду 4k+1 заздалагідь невідомий і треба вирішити, чи то спочатку організувати пошук простих виду 4k+1, сформувати базу, а потім у завданні для клієнта просто віддавати набори простих чисел, які треба комбінаторно перебрати, аби не змушувати шукати прості числа числа. Чи то залишити за клієнтом задачу пошуку простих чисел виду 4k+1 у заданому діапазоні. Я особисто схильний до того, щоб клієнти не займалися пошуками простих чисел, а лише перебирали всі їх комбінації. Як показує моя практика, якщо вже є якийсь, назвемо базовий набір простих, чисел, наприклад (73, 53^2), то для клієнта буде достатньо роботи, аби утворити і перевірити всі комбінації простих чисел виду 4k+1 із множини (5, 13, 17, 29, 37, 41) у всіх різноманітних їх ступенях у комбінації з базовим набором, так, що їх загальний добуток менший за 2^64. Тому я пропоную завдання для клієнта формувати наступним чином: (базовий набір) ; (динамічний набір). Так, наприклад завдання виду (53^2, 73) ; (5, 13, 17, 29, 37, 41) буде означати, що треба перебрати всі комбінації діагоналей, утворених добутком елементів базового набору (53^2, 73) з усіма можливими комбінаціями елементів динамічного набору (5, 13, 17, 29, 37, 41) в усіх можливих ступенях, таких, що загальний добуток менший за 2^64 За такої постановки задачі клієнти не будуть витрачати час на пошук простих чисел. Звичайно, що знайти наступне просте число виду 4k+1 не є великою проблемою для клієнта, якщо 4k+1, скажімо, менше за 1 000 000, але 1 000 000 - це тільки 2^20, а що робити, коли просте число буде порядку 2^50 і треба буде знайти наступне просте число? Клієнт вимушений буде витратити годину часу, аби тільки знайти, перевірити на простоту і, між іншим, лише задля того, щоб утворити з ним умовно кажучи пару-трійку комбінацій і впевнитись, що вони не утворюють Ідеального кубоїда. Дуже не ефективне використання ресурсів. Розмір динамічного діапазону залижить від елементів базового набору. Чим добуток елементів базового набору менший, тим менший має бути набір динамічного набору, адже за маленького добутку елементів базового набору ступенів свободи для динамічного набору більше. І навпаки. коли базовий набір буде рости і наближатися до 2^64, тим менше ступенів свободи у динамічного набору, а значить менша кількість діагоналей які треба перебрати, а отже, щоб завдання не було зовсім коротким, базовий набір для одного завдання буде складатися з великого за кількістю елементів базового набору великих простих чисел виду 4k+1. Ну, я сподіваюсь ви не позасинали, поки дочитали до звідси. В дійсності в цьомі проекті буде дуже багато математики, комбінаторики, теорії чисел і таке інше, тому звикайте Або не читайте і віддайте на потану тим, кому це цікаво. --------------------  (Show/Hide) |
  |
1 Користувачів переглядають дану тему (1 Гостей і 0 Прихованих Користувачів)
0 Користувачів:

|
Lo-Fi Версія | Поточний час: 29th January 2026 - 05:44 |




















